This section describes a general theorem for additive measurement in Fishburn (1992b) and applies it to the closed-interval representation
where 
and 
.
A sample of other approaches to interval and more general threshold
representations is provided in Doignon et al. (1986), Chateauneuf (1987),
Nakamura (1988), Suppes et al. (1989, Chapter 16),
Beja and Gilboa (1992),
Abbas and Vincke (1993),
Bogart and Trenk (1994), Abbas (1995) and Mitas (1995).
Our theorem is a linear separation theorem for arbitrary systems of
linear inequalities that have finite numbers of terms.
We begin with a nonempty set Y, and let V denote the vector
space of all 
for which
is finite. We define 
and v + v' for real 
and 
by
The representation for the theorem consists of distinguished subsets A
and B of V and a mapping 
for which
where 
.
We say that (A,B) is solvable if there exists a 
that satisfies linear system (10).
We will state a condition on (A,B) that is necessary and
sufficient
for solvability.
It is assumed, with no loss of generality, that the zero function 0
of V is in A and that B is not empty.
A few other definitions are needed.
For 
,
.
A subset K of V is a convex cone if it is nonempty,
closed under convex combinations, and contains
whenever 
and 
.
A convex cone K is without origin if 
.
The convex cone generated by nonempty 
is denoted
by 
, so
Finally, we say that nonempty is Archimedean
if for all 
, 
for some .
Our separation theorem says that (A,B) is solvable
if and only if 
is included in some Archimedean
convex cone without origin in V.
Given (10), necessity of the condition on
is shown by extending
linearly to all of V by 
and observing that 
is an Archimedean convex cone
without origin that includes .
The sufficiency proof is based on a standard separation theorem
discussed, for example, in Kelley and Namioka (1963) and Klee (1969).
To apply the theorem to the opening representation of this section,
let X' be a disjoint copy of X with 
corresponding to 
, and let 
.
The opening representation can then be rewritten as
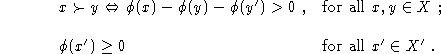
Sets A and B for application of the separation theorem are
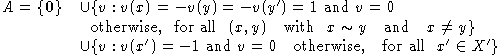
Suppose is included in an Archimedean convex cone without origin.
Let satisfy (10).
Then, when 
and 
,
and
, or 
and
;
for ,
,
or 
;
when 
,
, or
.
