A fundamental result for ![]() says that if X is countable then
there is a utility function
says that if X is countable then
there is a utility function ![]() such that
such that
if and only if ![]() on X is a weak order.
In this case, u is unique up to an ordinal transformation.
Sufficiency of weak order can be seen by enumerating the
indifference classes in
on X is a weak order.
In this case, u is unique up to an ordinal transformation.
Sufficiency of weak order can be seen by enumerating the
indifference classes in ![]() as
as ![]() , defining
, defining ![]() on
on ![]() by
by
![]()
noting that ![]() if
if
![]() , and then
defining u on X by
, and then
defining u on X by ![]() whenever
whenever ![]() .
.
Weak order is not generally sufficient for (1) when
![]() is uncountable.
For example, the linear order
is uncountable.
For example, the linear order ![]() on
on ![]() defined by
defined by ![]() if
if
![]() or
or
![]() can be represented lexicographically as
can be represented lexicographically as ![]() ,
where
,
where ![]() and
and
![]() denotes lexicographic order.
But it cannot be represented by (1):
otherwise, since
denotes lexicographic order.
But it cannot be represented by (1):
otherwise, since ![]() whenever
whenever ![]() , every interval
, every interval ![]() would contain a different rational number and yield the
contradiction that the countable set of rational numbers is uncountable.
would contain a different rational number and yield the
contradiction that the countable set of rational numbers is uncountable.
To obtain (1) when ![]() is uncountable, it needs to be
assumed also that
is uncountable, it needs to be
assumed also that ![]() includes a countable
subset that is
includes a countable
subset that is ![]() -order dense in
-order dense in ![]() .
By definition,
.
By definition, ![]() is order dense in
is order dense in ![]() if,
whenever
if,
whenever ![]() for
for
![]() , there is a
, there is a ![]() such that
such that
![]() .
Countable order denseness is often replaced in economic discussions by a
sufficient but nonnecessary topological assumption which implies
that u in (1) can defined to be continuous in the topology used for X.
.
Countable order denseness is often replaced in economic discussions by a
sufficient but nonnecessary topological assumption which implies
that u in (1) can defined to be continuous in the topology used for X.
Because (1) implies that ![]() is a weak order, it cannot
hold when
is a weak order, it cannot
hold when ![]() is acyclic or a partial order that is not also a weak order.
We can, however, continue to use u to preserve
is acyclic or a partial order that is not also a weak order.
We can, however, continue to use u to preserve ![]() one-way in the manner
one-way in the manner
![]() .
We can also use the same u to fully preserve, by equality, the strong
indifference relation
.
We can also use the same u to fully preserve, by equality, the strong
indifference relation ![]() on X defined by
on X defined by
![]()
for ![]() on X is an equivalence relation with
on X is an equivalence relation with ![]() and
and ![]() .
Thus, if X is countable, there is a
.
Thus, if X is countable, there is a ![]() for which
for which
if and only if ![]() on X is acyclic.
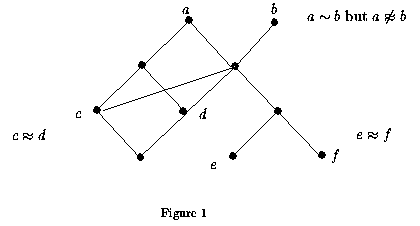
Figure 1 illustrates
on X is acyclic.
Figure 1 illustrates ![]() on a Haase diagram for a partially ordered
set in which one point bears
on a Haase diagram for a partially ordered
set in which one point bears ![]() to a second if there is a
downward sequence of lines from the first to the second.
to a second if there is a
downward sequence of lines from the first to the second.
When ![]() is uncountable, (2) holds for acyclic
is uncountable, (2) holds for acyclic
![]() if
if ![]() , defined in the natural way on
, defined in the natural way on ![]() , has a
linear extension in which some countable subset is order dense.
Further discussion along this line is available in Peleg (1970)
and Sondermann (1980).
, has a
linear extension in which some countable subset is order dense.
Further discussion along this line is available in Peleg (1970)
and Sondermann (1980).
Suppose ![]() is a partially ordered set that is not necessarily
weakly ordered.
An alternative to (2) of the two-way or
if and only if variety that replaces u in (1) by
another quantitative construct may then apply if
is a partially ordered set that is not necessarily
weakly ordered.
An alternative to (2) of the two-way or
if and only if variety that replaces u in (1) by
another quantitative construct may then apply if ![]() has additional structure.
A case of this occurs when
has additional structure.
A case of this occurs when ![]() is an
interval order, i.e., when
is an
interval order, i.e., when
![]()
The primary two-way representation for an interval order is
where ![]() with
with ![]() the set of all real intervals,
and for
the set of all real intervals,
and for ![]() , A > B means that a > b for all
, A > B means that a > b for all ![]() and all
and all ![]() .
One basic result (Fishburn 1970, Theorem 2.7) is: if
.
One basic result (Fishburn 1970, Theorem 2.7) is: if ![]() is
countable for an interval order
is
countable for an interval order ![]() , then (3) holds
for a mapping I into nondegenerate closed intervals.
Other structures may require open or half-open intervals (consider
, then (3) holds
for a mapping I into nondegenerate closed intervals.
Other structures may require open or half-open intervals (consider
![]() with
with ![]() ), and yet others may fail for (3) because
there are not enough intervals in
), and yet others may fail for (3) because
there are not enough intervals in ![]() to accommodate the desired
representation.
Further results are in Fishburn (1985, Chapter 7),
Peris and Subiza (1995), Bosi and Isler (1995),
and other references cited there.
to accommodate the desired
representation.
Further results are in Fishburn (1985, Chapter 7),
Peris and Subiza (1995), Bosi and Isler (1995),
and other references cited there.