| Previous | Table of Contents | Next |
A multiplicity is a definition of an inclusive interval of non-negative integers beginning with a lower bound and ending with
a (possibly infinite) upper bound. A multiplicity element embeds this information to specify the allowable cardinalities for
an instantiation of this element.
Description
A MultiplicityElement is an abstract metaclass which includes optional attributes for defining the bounds of a multiplicity.
A MultiplicityElement also includes specifications of whether the values in an instantiation of this element must be unique
or ordered.
Generalizations
•
“Element? on page 44
Attributes
• isOrdered: Boolean For a multivalued multiplicity, this attribute specifies whether the values in an instantiation of this element are sequentially ordered. Default is false.
• isUnique : Boolean For a multivalued multiplicity, this attributes specifies whether the values in an instantiation of this element are unique. Default is true.
• lower : Integer [0..1] Specifies the lower bound of the multiplicity interval. Default is one.
• upper : UnlimitedNatural [0..1] Specifies the upper bound of the multiplicity interval. Default is one.
Associations
No additional associations
Constraints
These constraint must handle situations where the upper bound may be specified by an expression not computable in the model.
In this package such situations cannot arise but they can in subclasses.
[1] A multiplicity must define at least one valid cardinality that is greater than zero.
upperBound()->notEmpty() implies upperBound() > 0
[2] The lower bound must be a non-negative integer literal.
lowerBound()->notEmpty() implies lowerBound() >= 0
[3] The upper bound must be greater than or equal to the lower bound.
(upperBound()->notEmpty() and lowerBound()->notEmpty()) implies upperBound() >= lowerBound()
Additional Operations
[1] The query isMultivalued() checks whether this multiplicity has an upper bound greater than one.
MultiplicityElement::isMultivalued() : Boolean;pre: upperBound()->notEmpty()isMultivalued = (upperBound() > 1)
[2] The query includesCardinality() checks whether the specified cardinality is valid for this multiplicity.
MultiplicityElement::includesCardinality(C : Integer) : Boolean;pre: upperBound()->notEmpty() and lowerBound()->notEmpty()includesCardinality = (lowerBound() <= C) and (upperBound() >= C)
[3] The query includesMultiplicity() checks whether this multiplicity includes all the cardinalities allowed by the specified
multiplicity.
MultiplicityElement::includesMultiplicity(M : MultiplicityElement) : Boolean;pre: self.upperBound()->notEmpty() and self.lowerBound()->notEmpty()and M.upperBound()->notEmpty() and M.lowerBound()->notEmpty()includesMultiplicity = (self.lowerBound() <= M.lowerBound()) and (self.upperBound() >= M.upperBound())
[4] The query lowerBound() returns the lower bound of the multiplicity as an integer.
MultiplicityElement::lowerBound() : [Integer];lowerBound = if lower->notEmpty() then lower else 1 endif
[5] The query upperBound() returns the upper bound of the multiplicity for a bounded multiplicity as an unlimited natural.
MultiplicityElement::upperBound() : [UnlimitedNatural];upperBound = if upper->notEmpty() then upper else 1 endif
Semantics
A multiplicity defines a set of integers that define valid cardinalities. Specifically, cardinality C is valid for multiplicity
M if M.includesCardinality(C).
A multiplicity is specified as an interval of integers starting with the lower bound and ending with the (possibly infinite)
upper bound.
If a MultiplicityElement specifies a multivalued multiplicity, then an instantiation of this element has a set of values.
The multiplicity is a constraint on the number of values that may validly occur in that set.
If the MultiplicityElement is specified as ordered (i.e., isOrdered is true), then the set of values in an instantiation of
this element is ordered. This ordering implies that there is a mapping from positive integers to the elements of the set of
values. If a MultiplicityElement is not multivalued, then the value for isOrdered has no semantic effect.
If the MultiplicityElement is specified as unordered (i.e., isOrdered is false), then no assumptions can be made about the
order of the values in an instantiation of this element.
If the MultiplicityElement is specified as unique (i.e., isUnique is true), then the set of values in an instantiation of
this element must be unique. If a MultiplicityElement is not multivalued, then the value for isUnique has no semantic effect.
Notation
The specific notation for a MultiplicityElement is defined by the concrete subclasses. In general, the notation will include
a multiplicity specification is shown as a text string containing the bounds of the interval, and a notation for showing the
optional ordering and uniqueness specifications.
The multiplicity bounds are typically shown in the format:
<lower-bound>’..’ <upper-bound>
where <lower-bound> is a non-negative integer and <upper-bound> is an unlimited natural number. The asterisk (*) is used as
part of a multiplicity specification to represent the unlimited (or infinite) upper bound.
If the Multiplicity is associated with an element whose notation is a text string (such as an attribute, etc.), the multiplicity
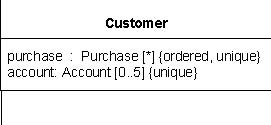
string will be placed within square brackets ([]) as part of that text string. Figure 9.33 shows two multiplicity strings
as
part of attribute specifications within a class symbol.
If the Multiplicity is associated with an element that appears as a symbol (such as an association end), the multiplicity
string is displayed without square brackets and may be placed near the symbol for the element. Figure 9.34 shows two
multiplicity strings as part of the specification of two association ends.
The specific notation for the ordering and uniqueness specifications may vary depending on the specific subclass of MultiplicityElement.
A general notation is to use a property string containing ordered or unordered to define the ordering, and unique or nonunique
to define the uniqueness.
Presentation Options
If the lower bound is equal to the upper bound, then an alternate notation is to use the string containing just the upper
bound. For example, “1? is semantically equivalent to “1..1.?
A multiplicity with zero as the lower bound and an unspecified upper bound may use the alternative notation containing a single
asterisk “*? instead of “0..*?.
The following BNF defines the syntax for a multiplicity string, including support for the presentation options listed above.
<multiplicity> ::= <multiplicity-range><multiplicity-range> ::= [ <lower> ‘..’ ] <upper><lower> ::= <integer><upper> ::= ‘*’ | <unlimited_natural>
Examples

Figure 9.33 - Multiplicity within a textual specification

Figure 9.34 - Multiplicity as an adornment to a symbol Rationale
MultiplicityElement represents a design trade-off to improve some technology mappings (such as XMI).